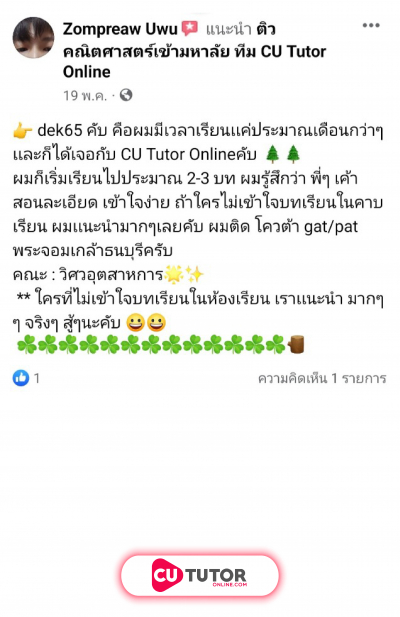
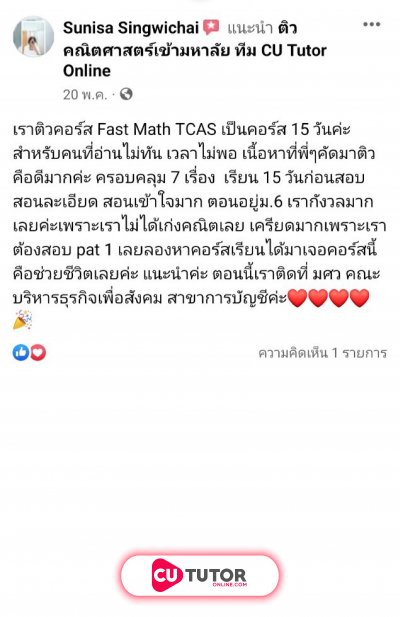
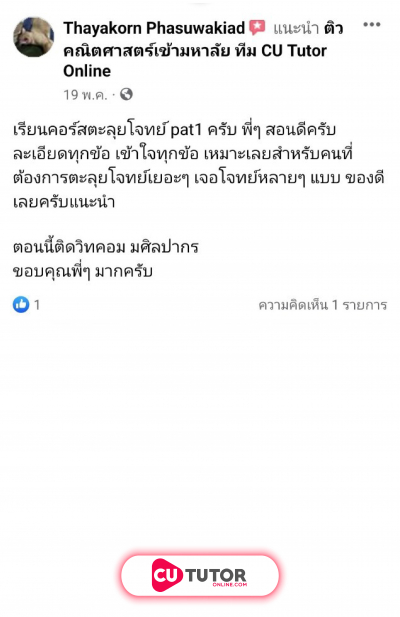
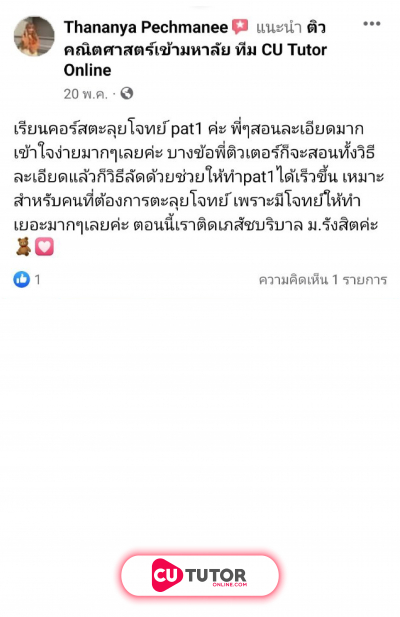
กำหนดให้ เป็นเส้นตรงผ่านจุด มีความชันเป็นจำนวนเต็มบวก และตัดแกน และแกน ที่จุด และจุด ตามลำดับ โดยผลบวกของระยะตัดแกน และระยะตัดแกน เท่ากับ หน่วย ให้ เป็นเส้นตรงที่ขนานกับเส้นตรง และผ่านจุด ถ้า เป็นจุดบนเส้นตรง โดยที่ แล้วพื้นที่ของรูปสามเหลี่ยม เท่ากับข้อใดต่อไปนี้

.jpg)
.jpg)