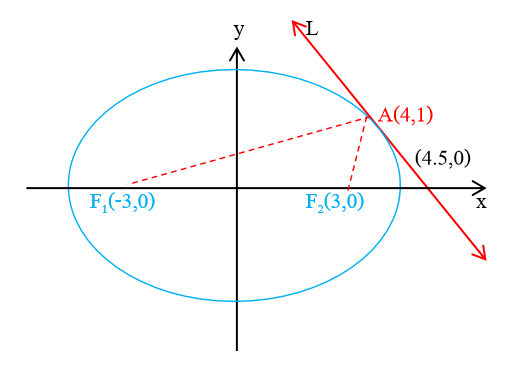
กำหนดให้วงรีมีจุดศูนย์กลางอยู่ที่ และมีโฟกัส และ อยู่บนแกน x จุด เป็นจุดบนวงรีโดยที่ผลบวกระยะทางจากจุด ไปยังจุดโฟกัสทั้งสองมีค่าเท่ากับ ให้เส้นตรง L ตัดแกน x ที่จุด และสัมผัสกับวงรีที่จุด ถ้า d เป็นระยะห่างระหว่างจุด กับเส้นตรง L แล้ว ค่าของ เท่ากับเท่าใด