ให้ แทนเซตของจำนวนจริง ให้
และ
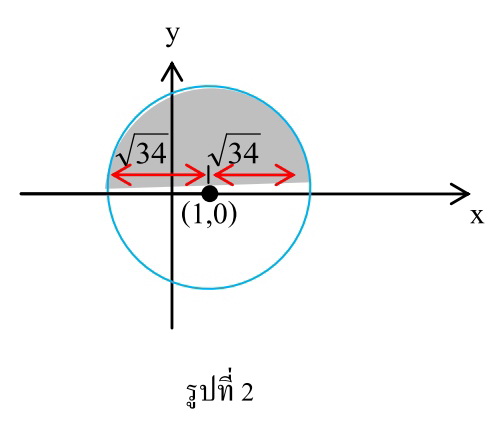
ถ้าโดเมนของเซต คือช่วงปิด เมื่อ และ เป็นจำนวนจริง โดยที่ แล้วค่าของ เท่ากับเท่าใด
ให้ แทนเซตของจำนวนจริง ให้
และ
ถ้าโดเมนของเซต คือช่วงปิด เมื่อ และ เป็นจำนวนจริง โดยที่ แล้วค่าของ เท่ากับเท่าใด
.jpg)
.jpg)
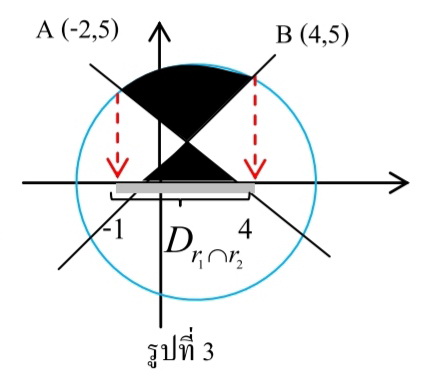
หลังจากนั้นนำกรณี 1 และกรณี 2 มารวมกัน
.jpg)