ข้อสอบ A-Level คณิตประยุกต์ 1 ปี 2564 (หลักสูตรใหม่)

ข้อ 29

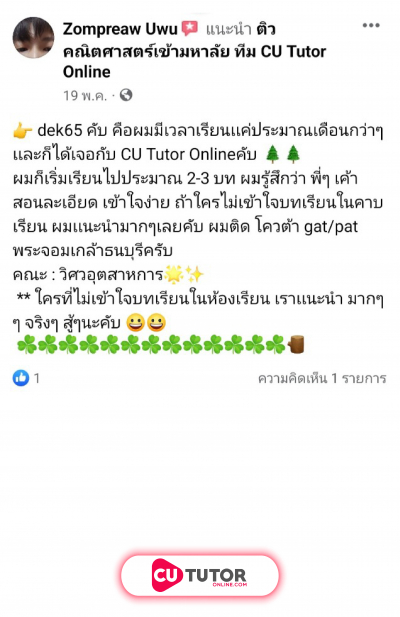
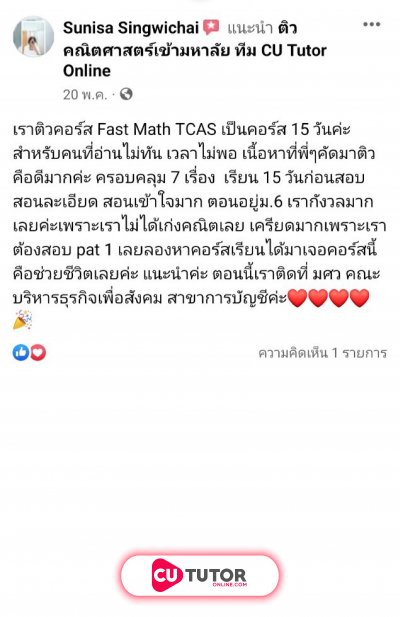
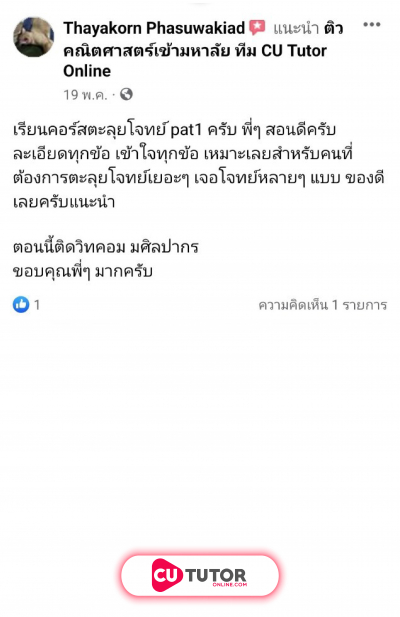
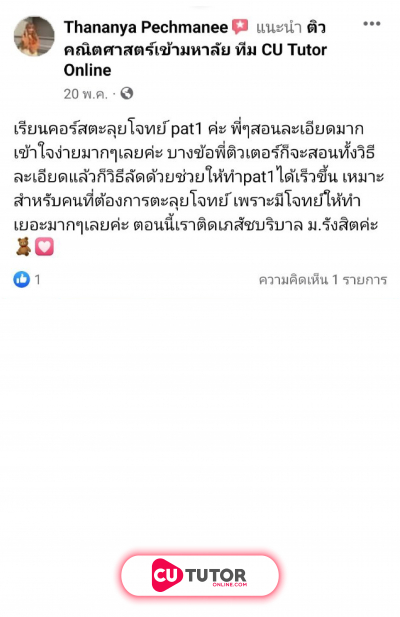
นักเรียนห้องหนึ่งมีจำนวน $50$ คน ในการสอบวิชาคณิตศาสตร์ มีนักเรียนเข้าสอบทั้งหมด $49$ คน ขาดสอบ $1$ คน โดยส่วนเบี่ยงเบนมาตรฐานของคะแนนสอบของนักเรียน $49$ คน เท่ากับ $10$ คะแนน ต่อมา นักเรียนที่ขาดสอบได้ขอสอบในภายหลัง เมื่อนำคะแนนของนักเรียนที่ขาดสอบมาคำนวณค่าเฉลี่ยเลขคณิตด้วย พบว่า ค่าเฉลี่ยเลขคณิตไม่มีการเปลี่ยนแปลง ความแปรปรวนของคะแนนสอบของนักเรียนทั้ง $50$ คน เท่ากับกี่ ${คะแนน}^{2}$

รีวิว - เสียงตอบรับจากผู้เรียน

เฉลยข้อสอบ

$จากสูตร σ = \sqrt{\frac{\sum_{i = 1}^{N} {(x_{i} - μ)}^{2}}{N}} \to 1 โดย σ = ส่วนเบี่ยงเบนมาตรฐาน μ = ค่าเฉลี่ยเลขคณิต$

$จากโจทย์ มีนักเรียนเข้าสอบทั้งหมด 49 คน ส่วนเบี่ยงเบนมาตรฐาน เท่ากับ 10 คะแนน จะได้ N = 49, σ = 10$

$จาก 1 จะได้ 10 = \sqrt{\frac{\sum_{i = 1}^{49} {(x_{i} - μ)}^{2}}{49}} 100 = \frac{\sum_{i = 1}^{49} {(x_{i} - μ)}^{2}}{49} \sum_{i = 1}^{49} {(x_{i} - μ)}^{2} = 4900$

$จากสูตร μ = \frac{\sum x_{i}}{N} μ = \frac{\sum x_{i}}{49}$

$จากโจทย์ นักเรียนที่ขาดสอบได้ขอสอบในภายหลัง พบว่า ค่าเฉลี่ยเลขคณิตไม่มีการเปลี่ยนแปลง จะได้ μ_{49 คน} = μ_{50 คน} แสดงว่า นักเรียนที่ขาดสอบ (คนที่ 50) มีคะแนน = μ$

$จาก 1 จะได้ σ_{50 คน} = \sqrt{\frac{\sum_{i = 1}^{50} {(x_{i} - μ)}^{2}}{50}} = \sqrt{\frac{\sum_{i = 1}^{49} {(x_{i} - μ)}^{2} + (x_{50} - μ)}{50}}$

$= \sqrt{\frac{4900 + (μ - μ)}{50}} = \sqrt{\frac{4900}{50}} = \sqrt{98} {σ^{2}}_{50 คน} = 98 ดังนั้น ความแปรปรวนของคะแนนสอบของนักเรียนทั้ง 50 คน = 98 {คะแนน}^{2}$

ข้อถัดไป