ข้อสอบ A-Level คณิตประยุกต์ 1 ปี 2565

ข้อ 20

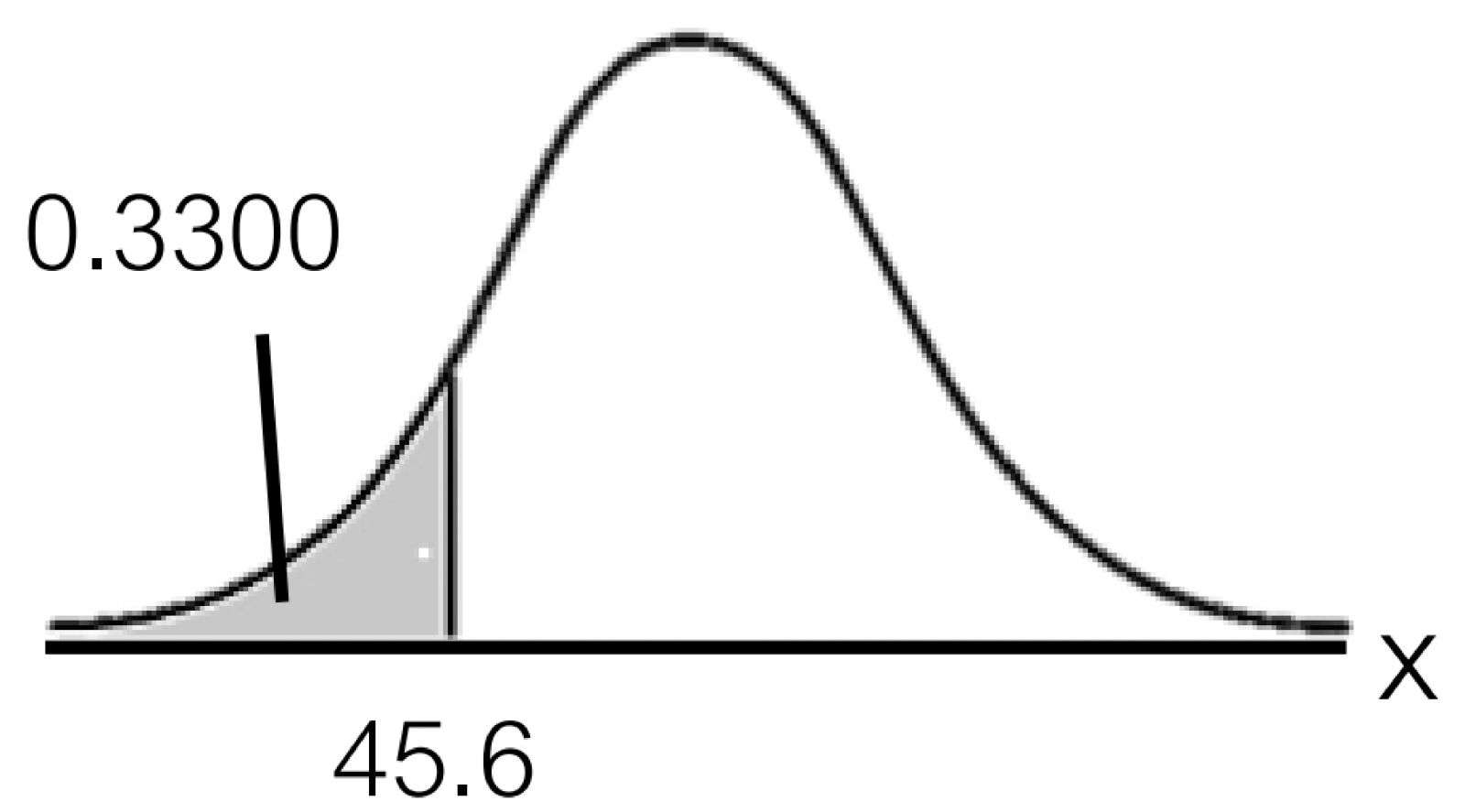
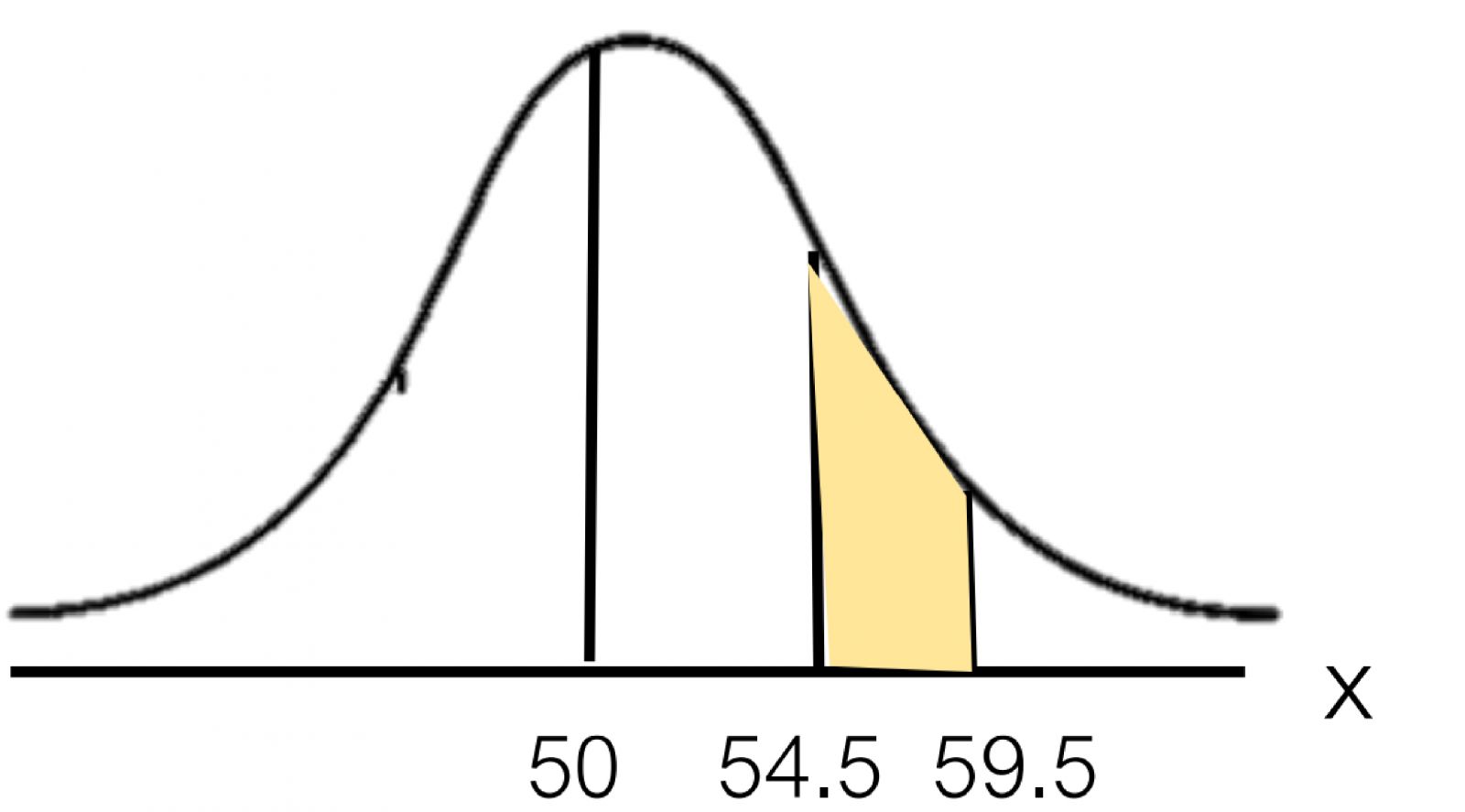
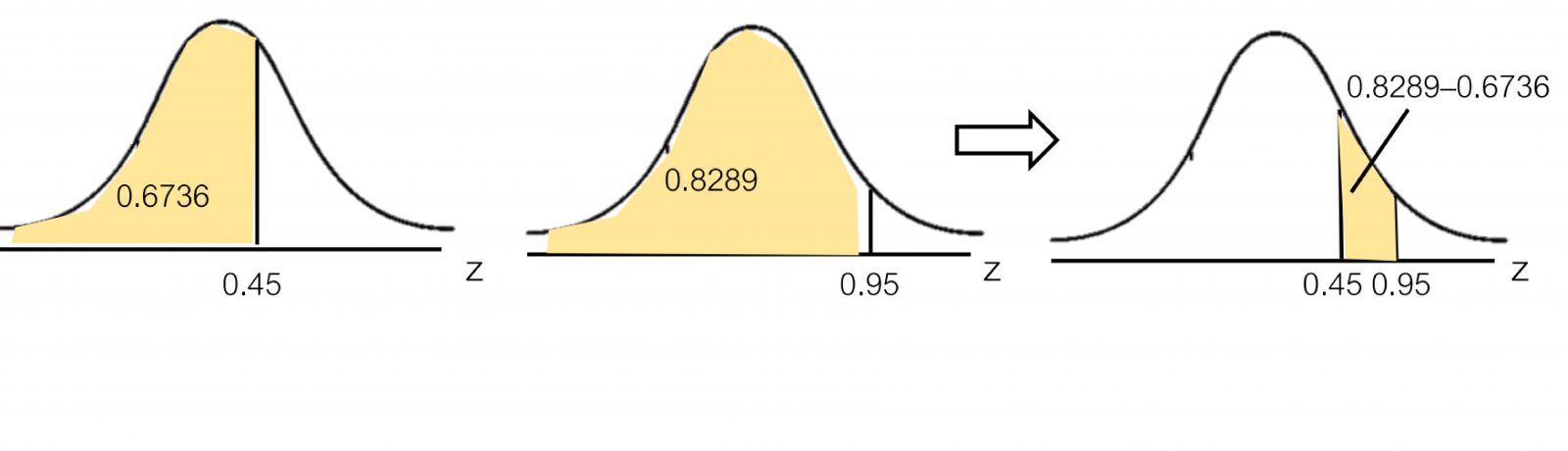
น้ำหนักของนักเรียนห้องหนึ่งมีการแจกแจงปกติ โดยมีค่าเฉลี่ยเป็น $5$ เท่าของส่วนเบี่ยงเบนมาตรฐาน และความน่าจะเป็นที่นักเรียนคนหนึ่งจะมีน้ำหนักน้อยกว่า $45.6$ กิโลกรัม เท่ากับ $0.3300$ ถ้าสุ่มนักเรียนในห้องนี้มา $1$ คน แล้วความน่าจะเป็นที่นักเรียนคนนี้จะมีน้ำหนักอยู่ระหว่าง $54.5$ ถึง $59.5$ กิโลกรัม เท่ากับเท่าใด

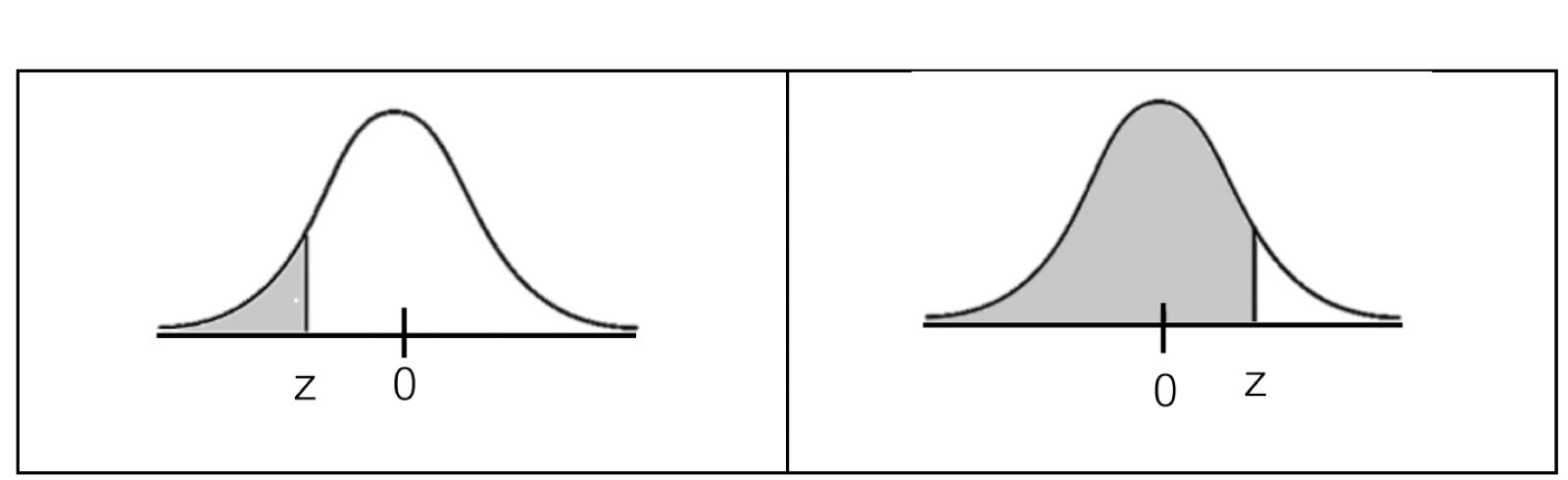
กำหนดตารางแสดงพื้นที่ใต้เส้นโค้งปกติมาตรฐาน ดังนี้

z

- 0.95

- 0.45

- 0.44

- 0.33

0.33

0.44

0.45

0.95

พื้นที่ใต้เส้นโค้ง

ปกติมาตรฐาน

0.1711

0.3264

0.3300

0.3707

0.6293

0.6700

0.6736

0.8289

1
$0.0407$
2
$0.0443$
3
$0.1553$
4
$0.1589$
5
$0.1711$

รีวิว - เสียงตอบรับจากผู้เรียน

เฉลยข้อสอบ

$จากเรื่องการแจกแจงปกติเราทราบว่า z = \frac{x - μ}{σ} จากโจทย์ μ = 5 σ โดย P (x < 45.6) = 0.3300$

$เทียบตารางจะได้ P (x < 45.6) = P (z < - 0.44) จาก z = \frac{x - μ}{σ} จะได้ว่า - 0.44 = \frac{45.6 - μ}{σ}$

$- 0.44 - σ = 45.6 - μ - 0.44 - σ = 45.6 - 5 σ 4.56 - σ = 45.6 σ = 10 จะได้ μ = 5 (10) = 50 โจทย์ต้องการความน่าจะเป็นของนักเรียนระหว่าง 54.5 - 59.5 กิโลกรัม$