ข้อสอบ PAT 1 - พฤศจิกายน 2557

ข้อ 11

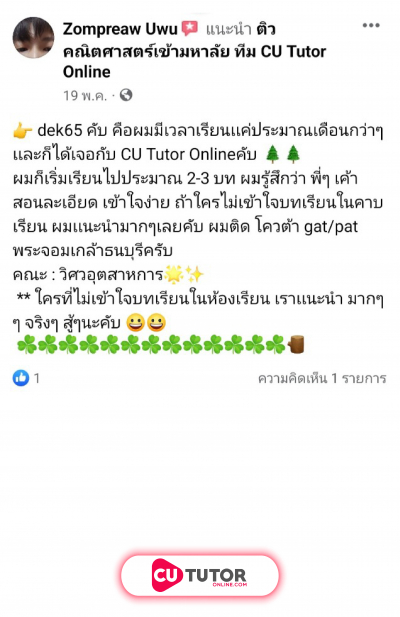
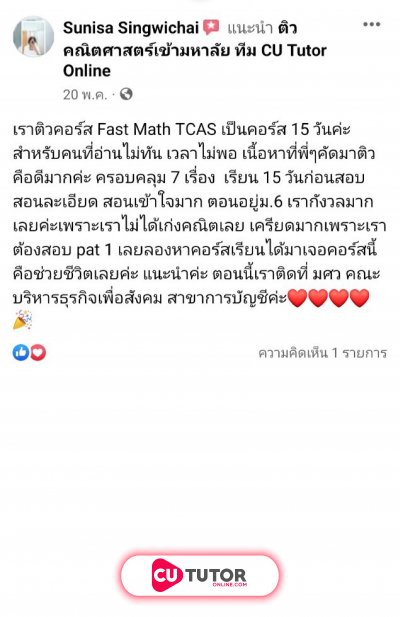
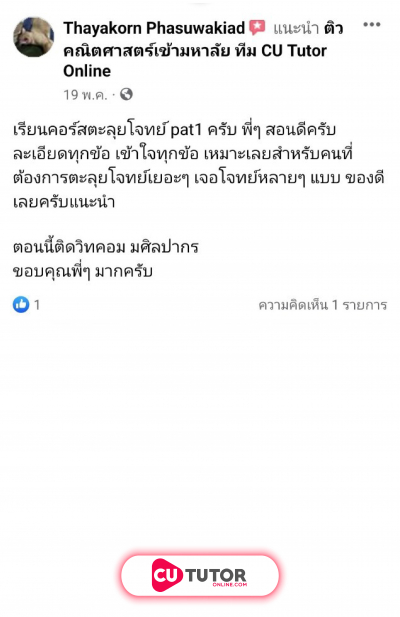
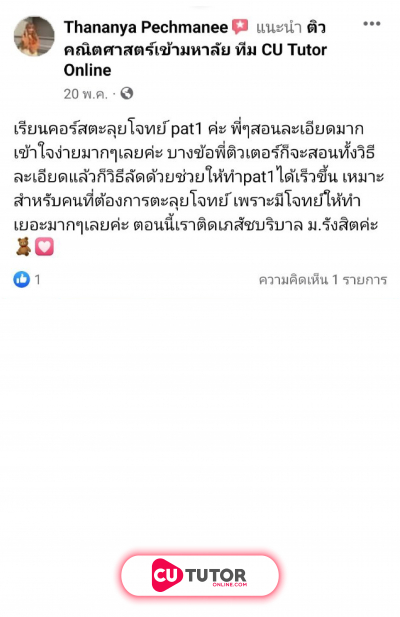
ให้ $C$ เป็นวงกลมมีสมการ $x^{2} + y^{2} + D x + E y + F = 0$ มีจุดศูนย์กลางอยู่ในควอดรันต์ (quadrant) ที่ 1 และวงกลม $C$ สัมผัสแกน $y$ ให้ $P$ เป็นพาราโบลามีสมการ $D x = y^{2} + E y + F$ ผ่านจุด $(- 4, - 1)$ และระยะระหว่างจุดยอดกับโฟกัสเท่ากับ 1 หน่วย พิจารณาข้อความต่อไปนี้
(ก) $D^{2} + E^{2} + F^{2} = 133$
(ข) เส้นตรง $4 x + 3 y - 7 = 0$ สัมผัสกับวงกลม $C$
ข้อใดต่อไปนี้ถูกต้อง

1
(ก) ถูก และ (ข) ถูก
2
(ก) ถูก แต่ (ข) ผิด
3
(ก) ผิด แต่ (ข) ถูก
4
(ก) ผิด และ (ข) ผิด

รีวิว - เสียงตอบรับจากผู้เรียน

เฉลยข้อสอบ

$จากโจทย์ C เป็นวงกลม x^{2} + y^{2} + Dx + Ey + F = 0 มีศูนย์กลางอยู่ในควอดรันต์ที่ 1 (Q_{1}) กำหนดให้ (a, b) เป็นจุดศูนย์กลางของวงกลม C จะได้ a > 0 และ b > 0 (เนื่องจาก Q_{1}) วงกลม C สัมผัสแกน y แสดงว่า วงกลมมีรัศมี a หน่วย - ลองวาดรูปวงกลม เพื่อความเข้าใจมากขึ้น$

$สูตรสมการวงกลม {(x - h)}^{2} + {(y - k)}^{2} = r^{2} - แทน h = a, k = b, r = a จะได้ {(x - a)}^{2} + {(y - b)}^{2} = a^{2} (x^{2} - 2 ax + a^{2}) + (y^{2} - 2 by + b^{2}) = a^{2} ดังนั้น x^{2} + y^{2} - 2 ax - 2 by + b^{2} = 0$

$เปรียบเทียบ ส . ป . ส . กับ x^{2} + y^{2} + Dx + Ey + F = 0 จะได้ D = - 2 a, E = - 2 b, F = b^{2} \to 1 a > 0 จะได้ D เป็นลบ จากโจทย์ P เป็นพาราโบลามีสมการ Dx = y^{2} + Ey + F จะได้ เป็นพาราโบลาเปิดด้านซ้าย เพราะ D เป็นลบ$

$สูตรพาราโบลา {(y - k)}^{2} = - 4 c (x - h) แทน c = - 1 (ระยะระหว่างจุดยอดกับโฟกัสเท่ากับ 1 หน่วย) y^{2} - 2 ky + k^{2} = - 4 (1) (x - h) y^{2} - 2 ky + k^{2} = - 4 x + 4 h - 4 x = y^{2} - 2 ky + k^{2} - 4 h$

$เปรียบเทียบ ส . ป . ส . กับ Dx = y^{2} + Ey + F จะได้ D = - 4, E = - 2 k, F = k^{2} - 4 h \to 2 จากโจทย์ P เป็นพาราโบลา ผ่านจุด (- 4, - 1) แทน (- 4, - 1) ในสมการพาราโบลา Dx = y^{2} + Ey + F แทน D = - 4, E = - 2 b, F = b^{2}$

$จะได้ (- 4) (- 4) = {(- 1)}^{2} + (- 2 b) (- 1) + b^{2} 16 = 1 + 2 b + b^{2} 0 = b^{2} + 2 b - 15 0 = (b + 5) (b - 3) b = - 5, 3; แต่ b > 0 b = 3 แทน b = 3 ใน 1 จะได้ E = - 2 b = - 2 (3) F = b^{2} = 3^{2} E = - 6 F = 9$

$(ก) จากโจทย์ D^{2} + E^{2} + F^{2} = {(- 4)}^{2} + {(- 6)}^{2} + 9^{2} = 133 ข้อ (ก) ถูก$

$(ข) จากโจทย์ เส้นตรง 4 x + 3 y - 7 = 0 สัมผัสกับวงกลม C จาก 1 D = - 2 a - 4 = - 2 a a = 2 จะได้ จุดศูนย์กลางวงกลม = (a, b) = (2, 3), รัศมี (a) = 2 - โดยเส้นตรงจะสัมผัสวงกลม เมื่อระยะจากศูนย์กลางไปเส้นตรง = รัศมี$

$จากสูตร ระยะจากจุด (x_{0}, y_{0}) ไปยังเส้นตรง {Ax}_{0} + {By}_{0} + C = 0 เท่ากับ d = \frac{|{Ax}_{0} + {By}_{0} + C|}{\sqrt{A^{2} + B^{2}}}$

$จะได้ ระยะจากจุด (2, 3) ไปยังเส้นตรง 4 x + 3 y - 7 = 0 เท่ากับ d = \frac{|4 (2) + 3 (3) - 7|}{\sqrt{4^{2} + 3^{2}}} = \frac{10}{5} = 2 ดังนั้น เส้นตรง 4 x + 3 y - 7 = 0 สัมผัสกับวงกลม C เนื่องจาก ระยะจากศูนย์กลางไปเส้นตรง = รัศมี ข้อ (ข) ถูก$

ข้อถัดไป